
- লেখক Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:34.
- সর্বশেষ পরিবর্তিত 2025-01-22 16:56.
বহুপদী পরিচয় ভেরিয়েবলের সমস্ত সম্ভাব্য মানের জন্য সঠিক সমীকরণ। উদাহরণস্বরূপ, x²+2x+1=(x+1)² হল একটি পরিচয় . এই ভূমিকা ভিডিও আরো উদাহরণ দেয় পরিচয় এবং আলোচনা করে কিভাবে আমরা একটি সমীকরণ প্রমাণ করি পরিচয়.
এর, বৈধ পরিচয় কি?
যদি একটি সমীকরণে এক বা একাধিক ভেরিয়েবল থাকে এবং হয় বৈধ ভেরিয়েবলের সমস্ত প্রতিস্থাপন মানের জন্য যার জন্য সমীকরণের উভয় দিক সংজ্ঞায়িত করা হয়েছে, তারপর সমীকরণটি একটি হিসাবে পরিচিত পরিচয় . সমীকরণ x 2 + 2 x = x(x + 2), উদাহরণস্বরূপ, একটি পরিচয় কারণ এটি হচ্ছে বৈধ x এর সমস্ত প্রতিস্থাপন মানের জন্য।
পরবর্তীকালে, প্রশ্ন হল, বহুপদী সূত্র কি? বহুপদী সমীকরণ সূত্র সাধারণত, দ বহুপদী সমীকরণ a আকারে প্রকাশ করা হয় (এক্স) উদাহরণ a বহুপদী সমীকরণ হল: 2x2 + 3x + 1 = 0, যেখানে 2x2 + 3x + 1 মূলত a বহুপদ অভিব্যক্তি যা শূন্যের সমান সেট করা হয়েছে, একটি গঠন করতে বহুপদী সমীকরণ.
উপরন্তু, বীজগণিতীয় পরিচয় কি?
একটি বীজগণিতীয় পরিচয় একটি সমতা যা এর ভেরিয়েবলের যেকোনো মান ধরে রাখে। উদাহরণস্বরূপ, দ পরিচয় (x + y) 2 = x 2 + 2 xy + y 2 (x+y)^2 = x^2 + 2xy + y^2 (x+y)2=x2+2xy+y2 x এর সমস্ত মানের জন্য ধারণ করে এবং y.
আপনি কিভাবে বীজগণিত পরিচয় যাচাই করবেন?
বীজগণিতীয় পরিচয় (a+b)2 = ক2 + 2ab + b2 যাচাই করা হয়। দ্য পরিচয় (a+b)2 = ক2 + 2ab + b2 কাগজ কাটা এবং পেস্ট দ্বারা যাচাই করা হয়. এই পরিচয় a এবং b এর অন্যান্য মান গ্রহণ করে জ্যামিতিকভাবে যাচাই করা যেতে পারে।
প্রস্তাবিত:
বীজগণিত 2-এ একটি পরিচয় কী?
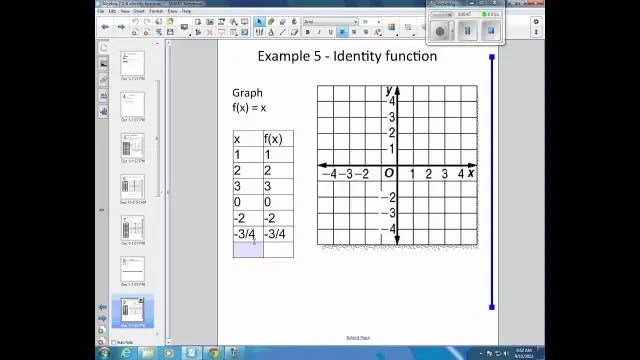
একটি পরিচয় সমীকরণ হল একটি সমীকরণ যা ভেরিয়েবলে প্রতিস্থাপিত যেকোনো মানের জন্য সর্বদা সত্য। উদাহরণস্বরূপ, 2 (x + 1) = 2 x + 2 2(x+1)=2x+2 2(x+1)=2x+2 একটি পরিচয় সমীকরণ
বিযুক্ত গণিতে পরিচয় আইন কি?

তাই পরিচয় আইন, p∧T≡p, মানে যে কোনো বাক্য p-এর সাথে একটি নির্বিচারে টাউটোলজি T-এর সংমিশ্রণ সর্বদা p-এর মতো একই সত্য মান থাকবে (অর্থাৎ, p-এর সাথে যৌক্তিকভাবে সমতুল্য হবে)। এর মানে হল যে কোন বাক্য p এর সাথে একটি নির্বিচারে টাউটোলজি T এর সাথে বিভক্তি সর্বদা সত্য হবে (নিজেই একটি টাটলজি হবে)
একটি বহুপদী গ্রাফ ধনাত্মক বা ঋণাত্মক হলে আপনি কিভাবে বলবেন?
যদি ডিগ্রিটি বিজোড় হয় এবং অগ্রণী সহগ ধনাত্মক হয়, তাহলে গ্রাফের বাম দিকটি নিচের দিকে এবং ডান দিকটি উপরে নির্দেশ করে। যদি ডিগ্রিটি বিজোড় হয় এবং অগ্রণী সহগ ঋণাত্মক হয়, গ্রাফের বাম দিকটি উপরে এবং ডান দিকটি নীচে নির্দেশ করে
ব্রেইনলি বহুপদী ফাংশনের শেষ আচরণ কী?

বাম প্রান্ত নীচে এবং ডান প্রান্ত সহ গ্রাফ করুন। অগ্রণী সহগ ঋণাত্মক তারপর বাম প্রান্ত উপরে এবং ডান প্রান্তটি নীচে। অতএব, বহুপদী ফাংশনের বিজোড় ডিগ্রি রয়েছে এবং অগ্রণী সহগ হল ঋণাত্মক
বহুপদী সমীকরণের শিকড় নির্ণয় করার সময় বহুত্ব বিবেচনা করা কেন গুরুত্বপূর্ণ?

উদাহরণ স্বরূপ, একটি প্রদত্ত বহুপদী সমীকরণের একটি নির্দিষ্ট বিন্দুতে যতবার একটি রুট আছে তা হল সেই মূলের বহুগুণ। ব্যতিক্রম উল্লেখ না করে সঠিকভাবে গণনা করতে সক্ষম হওয়ার জন্য গুণের ধারণাটি গুরুত্বপূর্ণ (উদাহরণস্বরূপ, দ্বিগুণ মূল দুইবার গণনা করা হয়েছে)। তাই অভিব্যক্তি, 'গুণে গুণিত'
