ভিডিও: একটি ফাংশনের মূল বৈশিষ্ট্যগুলি কী কী?
2024 লেখক: Miles Stephen | [email protected]. সর্বশেষ পরিবর্তিত: 2023-12-15 23:34
মূল বৈশিষ্ট্য অন্তর্ভুক্ত: বাধা; ব্যবধান যেখানে ফাংশন বাড়ছে, কমছে, ইতিবাচক বা নেতিবাচক; আপেক্ষিক সর্বোচ্চ এবং সর্বনিম্ন; প্রতিসাম্য; শেষ আচরণ; এবং পর্যায়ক্রমিকতা।
এই বিষয়ে, ফাংশন বৈশিষ্ট্য কি?
একটি ফাংশন হল একটি সম্পর্ক যেখানে প্রতিটি সম্ভাব্য ইনপুট মান ঠিক একটি আউটপুট মান নিয়ে যায়। আমরা বলি "আউটপুট হল ইনপুটের একটি ফাংশন।" ইনপুট মান ডোমেন তৈরি করে, এবং আউটপুট মানগুলি তৈরি করে পরিসীমা.
অধিকন্তু, একটি গ্রাফের বৈশিষ্ট্যগুলি কী কী? একটি গ্রাফের প্রধান বৈশিষ্ট্যগুলি দেখানো একটি পোস্টার৷
- y-অক্ষ হল উল্লম্ব অক্ষ।
- x-অক্ষ হল অনুভূমিক অক্ষ।
- উৎপত্তি হল সেই বিন্দু যেখানে x-অক্ষ এবং y-অক্ষ উভয়ই শূন্য এবং ছেদ করে।
- শিরোনাম - গ্রাফে প্রদর্শিত তথ্য সম্পর্কিত।
ঠিক তাই, একটি দ্বিঘাত ফাংশনের মূল বৈশিষ্ট্যগুলি কী কী?
দ্য দ্বিঘাত ফাংশনের মূল বৈশিষ্ট্য y-ইন্টারসেপ্ট, প্রতিসাম্যের অক্ষ এবং টার্নিং পয়েন্টের (বা শীর্ষবিন্দু) স্থানাঙ্ক ও প্রকৃতি।
ফাংশন কিভাবে কাজ করে?
ক ফাংশন একটি সমীকরণ যার প্রতিটি x এর জন্য y এর জন্য একটি মাত্র উত্তর আছে। ক ফাংশন একটি নির্দিষ্ট ধরণের প্রতিটি ইনপুটে ঠিক একটি আউটপুট বরাদ্দ করে। এটি একটি নামকরণ সাধারণ ফাংশন হয় f(x) অথবা y এর পরিবর্তে g(x)। f(2) এর অর্থ হল আমাদের আমাদের মান খুঁজে বের করা উচিত ফাংশন যখন x 2 এর সমান হয়।
প্রস্তাবিত:
একটি ফাংশনের একটি অনুভূমিক স্পর্শক রেখা আছে কিনা আপনি কিভাবে নির্ধারণ করবেন?
অনুভূমিক রেখাগুলির একটি ঢাল শূন্য রয়েছে। অতএব, যখন ডেরিভেটিভ শূন্য হয়, স্পর্শক রেখাটি অনুভূমিক হয়। অনুভূমিক স্পর্শক রেখাগুলি খুঁজে পেতে, শূন্যগুলি সনাক্ত করতে ফাংশনের ডেরিভেটিভ ব্যবহার করুন এবং তাদের মূল সমীকরণে আবার প্লাগ করুন
একটি সূচকীয় ফাংশনের বিপরীত কি?
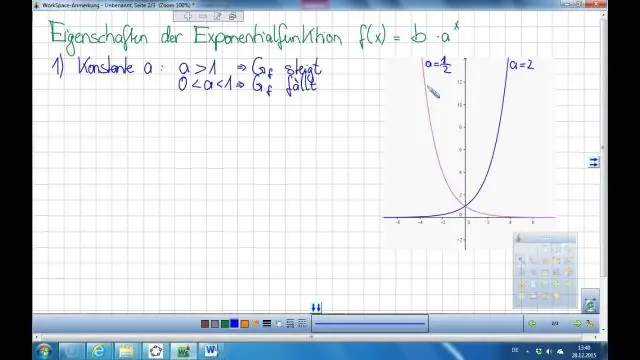
সূচকীয় ফাংশনের বিপরীত y = ax হল x = ay। লগারিদমিক ফাংশন y = logax কে সূচকীয় সমীকরণ x = ay এর সমতুল্য বলে সংজ্ঞায়িত করা হয়
একটি ফাংশনের বিপরীত কি?
একটি ফাংশনের বিপরীত একটি ফাংশন যা মূল ফাংশনের 'প্রভাব' বিপরীত করে। একটি ফাংশন দেওয়া হলে, f(x) বলুন, ফাংশনের ইনভার্স বের করতে, আমরা প্রথমে f(x) কে y এ পরিবর্তন করি। এর পরে, আমরা সমস্ত x থেকে y এবং y থেকে x পরিবর্তন করি। এবং তারপর আমরা y জন্য সমাধান. y এর প্রাপ্ত সমাধান হল মূল ফাংশনের বিপরীত
আপনি কিভাবে একটি দ্বিঘাত ফাংশনের প্রতীকী উপস্থাপনা খুঁজে পান?
দ্বিঘাত ফাংশনগুলিকে সমীকরণ দ্বারা প্রতীকীভাবে উপস্থাপন করা যেতে পারে, y(x) = ax2 + bx + c, যেখানে a, b, এবং c হল ধ্রুবক, এবং a ≠ 0. এই ফর্মটিকে স্ট্যান্ডার্ড ফর্ম হিসাবে উল্লেখ করা হয়
আপনি কিভাবে একটি কাজের ফাংশনের থ্রেশহোল্ড ফ্রিকোয়েন্সি খুঁজে পাবেন?
এটি গণনা করার জন্য, আপনার উপাদানটির উপর আলোর ঘটনার শক্তি এবং নির্গত ফটোইলেক্ট্রনের গতিশক্তির প্রয়োজন হবে। E = hf ব্যবহার করে আমরা শক্তিতে সাবব করে এবং f এর জন্য কাজ করে আলোর ফ্রিকোয়েন্সি বের করতে পারি। এটি থ্রেশহোল্ড ফ্রিকোয়েন্সি হবে