ভিডিও: আপনি কিভাবে একটি প্যারামেট্রিক সমীকরণের স্থিতিবিন্যাস খুঁজে পাবেন?
2024 লেখক: Miles Stephen | [email protected]. সর্বশেষ পরিবর্তিত: 2023-12-15 23:34
দ্য অভিমুখ সমতলের বক্ররেখা হিসাবে প্যারামিটার বৃদ্ধি বলা হয় অভিযোজন এর বক্ররেখা . দ্য অভিযোজন একটি সমতল বক্ররেখা বরাবর আঁকা তীর দ্বারা প্রতিনিধিত্ব করা যেতে পারে বক্ররেখা . নীচের গ্রাফ পরীক্ষা করুন. এটা দ্বারা সংজ্ঞায়িত করা হয় প্যারামেট্রিক সমীকরণ x = cos(t), y = sin(t), 0≦t < 2Π।
এখানে, আপনি কিভাবে একটি গ্রাফ এর ওরিয়েন্টেশন জানেন?
প্রতি চিত্রলেখ একটি অ্যাসাইক্লিক আছে অভিযোজন ; সব অ্যাসাইক্লিক অভিযোজন শীর্ষবিন্দুগুলিকে একটি অনুক্রমের মধ্যে স্থাপন করে এবং তারপর প্রতিটি প্রান্তকে তার শেষবিন্দুর আগের থেকে পরবর্তী প্রান্তে নির্দেশ করে প্রাপ্ত করা যেতে পারে।
উপরন্তু, একটি প্যারামিটারাইজেশন কি? গণিতে, এবং আরও বিশেষভাবে জ্যামিতিতে, পরামিতিকরণ (বা প্যারামিটারাইজেশন ; এছাড়াও প্যারামিটারাইজেশন , প্যারামেট্রিসেশন) হল একটি বক্ররেখা, একটি পৃষ্ঠ বা, আরও সাধারণভাবে, একটি বহুগুণ বা বিভিন্ন, একটি অন্তর্নিহিত সমীকরণ দ্বারা সংজ্ঞায়িত প্যারামেট্রিক সমীকরণগুলি খুঁজে বের করার প্রক্রিয়া।
তারপর, একটি প্যারামেট্রিক গ্রাফ কি?
তাই, ক প্যারামেট্রিক একটি পরামিতি নামক তৃতীয় চলকের অধীনে বক্ররেখার -কোঅর্ডিনেট এবং -কোঅর্ডিনেটের জন্য দুটি পৃথক ফাংশনের অধীনে বক্ররেখা সংজ্ঞায়িত করা হয়। প্রায়শই প্যারামিটার "" ব্যবহার করা হয় এবং প্রায়শই প্রতীকীভাবে "সময়" উপস্থাপন করতে ব্যবহৃত হয় যেহেতু একটি কণা একটি বক্ররেখা অতিক্রম করে।
ভেক্টর সমীকরণ কি?
ভেক্টর সমীকরণ একটি সরল রেখার কার্টেসিয়ান সমীকরণ একটি সরল রেখার জন্য হল y = mx + c, যেখানে m রেখার গ্রেডিয়েন্টকে প্রতিনিধিত্ব করে এবং c হল সেই বিন্দু যেখানে রেখাটি y-অক্ষ অতিক্রম করে। ক ভেক্টর সমীকরণ একটি লাইনের জন্য একইভাবে 2 টুকরো তথ্য প্রয়োজন: লাইনের একটি বিন্দু। লাইনের দিক।
প্রস্তাবিত:
আপনি কিভাবে একটি বৃত্তের একটি সেক্টরের দৈর্ঘ্য খুঁজে পাবেন?
একটি কেন্দ্রীয় কোণ যা একটি প্রধান চাপ দ্বারা উপস্থাপিত হয় তার পরিমাপ 180° এর চেয়ে বড়। একটি বৃত্তের একটি চাপের দৈর্ঘ্য খুঁজে পেতে চাপের দৈর্ঘ্যের সূত্রটি ব্যবহার করা হয়; l=rθ l = r θ, যেখানে θ রেডিয়ানে আছে। সেক্টর এলাকা পাওয়া যায় A=12θr2 A = 1 2 θ r 2, যেখানে θ রেডিয়ানে আছে
আপনি কিভাবে একটি স্থানাঙ্ক সমতলে একটি প্রসারণের স্কেল ফ্যাক্টর খুঁজে পাবেন?
স্থানাঙ্ক A(2, 6), B(2, 2), C(6, 2) সহ ত্রিভুজ ABC গ্রাফ কর। তারপরে প্রসারণের কেন্দ্র হিসাবে উত্স সহ 1/2 এর স্কেল ফ্যাক্টর দ্বারা চিত্রটিকে প্রসারিত করুন। প্রথমে, আমরা স্থানাঙ্ক সমতলে আমাদের মূল ত্রিভুজ গ্রাফ করি। এর পরে, আমরা প্রতিটি স্থানাঙ্ককে 1/2 এর স্কেল ফ্যাক্টর দ্বারা গুণ করি
আপনি কিভাবে লগারিদমিক সমীকরণের অ্যাসিম্পটোট খুঁজে পাবেন?
মূল পয়েন্টগুলি যখন গ্রাফ করা হয়, লগারিদমিক ফাংশনটি বর্গমূল ফাংশনের আকৃতিতে অনুরূপ, তবে x ডান দিক থেকে 0 এর কাছে যাওয়ার সাথে সাথে একটি উল্লম্ব অ্যাসিম্পটোট সহ। বিন্দু (1,0) হল y=logbx y = l o g b x ফর্মের সমস্ত লগারিদমিক ফাংশনের গ্রাফে, যেখানে b হল একটি ধনাত্মক বাস্তব সংখ্যা
আপনি কিভাবে একটি দ্বিঘাত ফাংশন একটি খুঁজে পাবেন?
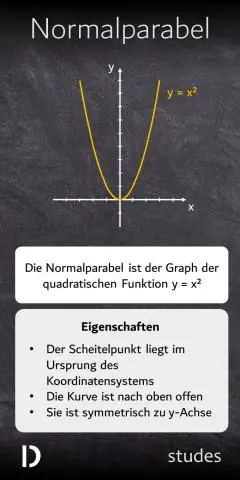
দ্বিঘাত ফাংশন f(x) = a(x -h)2 + k, a শূন্যের সমান নয়, বলা হয় স্ট্যান্ডার্ড ফর্মে। যদি a ধনাত্মক হয়, গ্রাফটি উপরের দিকে খোলে এবং যদি একটি ঋণাত্মক হয়, তবে এটি নীচের দিকে খোলে। প্রতিসাম্যের রেখা হল উল্লম্ব রেখা x = h, এবং শীর্ষবিন্দু হল বিন্দু(h,k)
আপনি কিভাবে বীজগণিতভাবে একটি সমীকরণের শিকড় খুঁজে পাবেন?
যেকোনো দ্বিঘাত সমীকরণের মূলগুলি দেওয়া হয়: x = [-b +/- sqrt(-b^2 - 4ac)]/2a। দ্বিঘাতটিকে ax^2 + bx + c = 0 আকারে লিখুন। যদি সমীকরণটি y = ax^2 + bx +c আকারে থাকে তবে কেবল y-এর পরিবর্তে 0 দিন। এটি করা হয়েছে কারণ এর মূল সমীকরণ হল সেই মান যেখানে y অক্ষ 0 এর সমান