ভিডিও: একটি পাটিগণিত সিরিজের যোগফল কি ঋণাত্মক হতে পারে?
2024 লেখক: Miles Stephen | [email protected]. সর্বশেষ পরিবর্তিত: 2023-12-15 23:34
এর আচরণ গাণিতিক ক্রম সাধারণ পার্থক্যের উপর নির্ভর করে d. যদি সাধারণ পার্থক্য, d, হয়: ধনাত্মক, the ক্রম হবে অনন্তের দিকে অগ্রগতি (+∞) নেতিবাচক , দ্য ক্রম হবে দিকে প্রত্যাবর্তন নেতিবাচক অনন্ত (−∞)
তাছাড়া ধারার যোগফল কি ঋণাত্মক হতে পারে?
আপনি সম্পর্কে কথা বলছেন যোগফল একটি অসীম সিরিজ যা বোঝায় যে সিরিজ জ্যামিতিক, যেহেতু একটি অসীম পাটিগণিত সিরিজ করতে পারেন কখনও একত্রিত হয় না। মনে রাখবেন, সাধারণ অনুপাত হতে হবে |r| < 1 ক জন্য যোগফল অস্তিত্ব এইভাবে যদি সাধারণ অনুপাত সেখানে ধনাত্মক হয় করতে পারা না হতে ঋণাত্মক যোগফল.
এছাড়াও, সসীম পাটিগণিত সিরিজের যোগফল কত? দ্য যোগফল of (n) একটি এর পদ পাটিগণিত সিরিজ (n) এর সমস্ত মানের জন্য (5{n}^{2}-11n) হল। সাধারণ পার্থক্য নির্ধারণ করুন। দ্য যোগফল একটি পাটিগণিত সিরিজ (ext{100}) তার প্রথম মেয়াদের বার, যখন শেষ পদটি (ext{9}) বার প্রথম মেয়াদের।
এর, আপনি কিভাবে একটি পাটিগণিত সিরিজের যোগফল খুঁজে পাবেন?
প্রতি অনুসন্ধান দ্য যোগফল একটি পাটিগণিত ক্রম, অনুক্রমের প্রথম এবং শেষ সংখ্যা সনাক্ত করে শুরু করুন। তারপর, সেই সংখ্যাগুলিকে একসাথে যোগ করুন এবং ভাগ করুন যোগফল 2 দ্বারা। অবশেষে, সেই সংখ্যাটিকে অনুক্রমের মোট পদ সংখ্যা দ্বারা গুণ করুন অনুসন্ধান দ্য যোগফল.
সিরিজে N কি?
প্রথম পদ a1, সাধারণ পার্থক্য হল d, এবং পদ সংখ্যা হল। একটি পাটিগণিতের যোগফল সিরিজ প্রথম এবং শেষ পদের গড় পদের সংখ্যাকে গুণ করে পাওয়া যায়। খুঁজে বের করতে, একটি পাটিগণিতের জন্য সুস্পষ্ট সূত্র ব্যবহার করুন ক্রম . আমরা = 25 পেতে 3 + (– 1)·4 = 99 সমাধান করি।
প্রস্তাবিত:
চি বর্গ কি ঋণাত্মক হতে পারে?
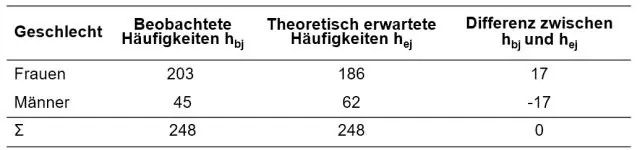
আপনি কি বলতে চাচ্ছেন: চি স্কোয়ারের মান কি কখনো ঋণাত্মক হতে পারে? উত্তর হল না। একটি চি বর্গক্ষেত্রের মান ঋণাত্মক হতে পারে না কারণ এটি বর্গ পার্থক্যের যোগফলের উপর ভিত্তি করে (প্রাপ্ত এবং প্রত্যাশিত ফলাফলের মধ্যে)
পাটিগণিত সিরিজের যোগফল কত?
একটি পাটিগণিত সিরিজের যোগফল প্রথম এবং শেষ পদের গড় পদের সংখ্যাকে গুণ করে পাওয়া যায়। উদাহরণ: 3 + 7 + 11 + 15 + ··· + 99 এর রয়েছে a1 = 3 এবং d = 4
আপনি কিভাবে একটি সসীম পাটিগণিত বা জ্যামিতিক সিরিজের যোগফল খুঁজে পাবেন?
জ্যামিতিক অনুক্রমের n পদগুলির যোগফলের সূত্রটি Sn = a[(r^n - 1)/(r - 1)] দ্বারা দেওয়া হয়েছে, যেখানে a হল প্রথম পদ, n হল পদ সংখ্যা এবং r হল সাধারণ অনুপাত
কোন দুটি ঋণাত্মক ক্রমাগত পূর্ণসংখ্যার যোগফল আছে?
দুটি ঋণাত্মক পরপর পূর্ণসংখ্যার যোগফল -21
জ্যামিতিক সিরিজের যোগফল কত?
একটি অসীম জ্যামিতিক সিরিজের যোগফলের জন্য, সাধারণ অনুপাত r অবশ্যই &মাইনাস;1 এবং 1-এর মধ্যে হতে হবে। একটি অসীম জ্যামিতিক সিরিজের সমষ্টি খুঁজে বের করতে যার অনুপাত একের চেয়ে কম একটি পরম মান আছে, সূত্রটি ব্যবহার করুন, S= a11−r, যেখানে a1 হল প্রথম পদ এবং r হল সাধারণ অনুপাত