2025 লেখক: Miles Stephen | [email protected]. সর্বশেষ পরিবর্তিত: 2025-01-22 16:56
করবেন আপনি মানে: করতে পারা এর মান চি বর্গক্ষেত্র কখনও হতে নেতিবাচক ? উত্তর হল না। a এর মান চি বর্গক্ষেত্র হতে পারে না নেতিবাচক কারণ এটি একটি যোগফলের উপর ভিত্তি করে বর্গক্ষেত্র পার্থক্য (প্রাপ্ত এবং প্রত্যাশিত ফলাফলের মধ্যে)।
একইভাবে, চি বর্গ বন্টন সবসময় ইতিবাচক কেন?
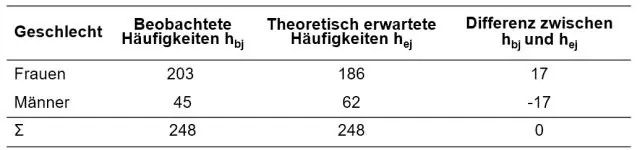
এর গণনা করা মান চি - বর্গক্ষেত্র হয় সবসময় ইতিবাচক কারণ পর্যবেক্ষণকৃত ফ্রিকোয়েন্সি এবং প্রত্যাশিত কম্পাঙ্কের মধ্যে পার্থক্য হল বর্গক্ষেত্র , অর্থাৎ (O - E)2 এবং demoninator হল প্রত্যাশিত সংখ্যা যা হতে হবে ইতিবাচক . দ্য চি - বর্গক্ষেত্র বিতরণ ইতিবাচকভাবে তির্যক।
উপরের পাশে, চি বর্গ কি 0 হতে পারে? পরিসংখ্যানে, অ-কেন্দ্রীয় চি - বর্গক্ষেত্র সঙ্গে বিতরণ শূন্য স্বাধীনতার মাত্রা করতে পারা নাল হাইপোথিসিস পরীক্ষা করার জন্য ব্যবহার করা হবে যে একটি নমুনা ব্যবধানে একটি অভিন্ন বন্টন থেকে এসেছে ( 0 , 1)। এটা তুচ্ছ যে একটি "কেন্দ্রীয়" চি সঙ্গে বর্গ বন্টন শূন্য স্বাধীনতার ডিগ্রী সব সম্ভাবনাকে কেন্দ্রীভূত করে শূন্য.
একইভাবে, আপনি একটি ঋণাত্মক T মান থাকতে পারে?
অনুমানের চেয়ে ছোট হলে মান , এরপর t - পরিসংখ্যান নেতিবাচক হবে . এটা বড় হলে, t - পরিসংখ্যান হবে ইতিবাচক ক নেতিবাচক চিহ্ন বোঝায় যে নমুনা গড় অনুমানকৃত গড় থেকে কম।
আপনি কিভাবে নাল হাইপোথিসিস চি স্কোয়ার প্রত্যাখ্যান করবেন?
অন্য কথায়, যখন গণনা করা x2 পরিসংখ্যান 0.05 সম্ভাব্যতা স্তরের জন্য টেবিলের সমালোচনামূলক মান অতিক্রম করে, তাহলে আমরা পারি শূন্য হাইপোথিসিস প্রত্যাখ্যান করুন সমান বন্টনের।
প্রস্তাবিত:
ভূমিকম্পের কতক্ষণ পরে আফটারশক হতে পারে?
মেনশকের দশ দিন পর আফটারশকের সংখ্যা মাত্র দশমাংশ। ভূমিকম্পকে আফটারশক বলা হবে যতক্ষণ পর্যন্ত ভূমিকম্পের হার মেইনশকের আগের তুলনায় বেশি থাকে। বড় ভূমিকম্পের জন্য এটি কয়েক দশক ধরে চলতে পারে। বড় ভূমিকম্পে বেশি এবং বড় আফটারশক হয়
একটি পাটিগণিত সিরিজের যোগফল কি ঋণাত্মক হতে পারে?
পাটিগণিত ক্রম আচরণ সাধারণ পার্থক্য উপর নির্ভর করে d. যদি সাধারণ পার্থক্য, d, হয়: ধনাত্মক, ক্রমটি অনন্ত (+∞) নেতিবাচকের দিকে অগ্রসর হবে, ক্রমটি ঋণাত্মক অসীমের দিকে ফিরে যাবে (−∞)
পাপ বর্গ x সমান sin x বর্গ?
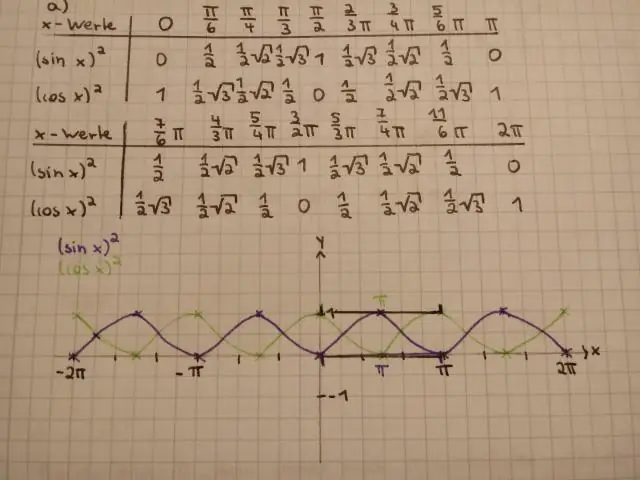
হ্যাঁ এটা. sin^2x একই assinx^2 কারণ উভয় ক্ষেত্রেই '^2' শুধুমাত্র x এর সাথে সম্পর্কিত
ঋণাত্মক সংখ্যার ঘনমূল ঋণাত্মক সংখ্যা কেন?
একটি ঋণাত্মক সংখ্যার ঘনমূল সর্বদা ঋণাত্মক হবে যেহেতু একটি সংখ্যাকে ঘন করার অর্থ হল এটিকে 3য় ঘাতে উন্নীত করা - যা বিজোড় - ঋণাত্মক সংখ্যার ঘনমূলগুলিও ঋণাত্মক হতে হবে। যখন সুইচ বন্ধ (নীল), ফলাফল নেতিবাচক হয়. যখন সুইচ চালু থাকে (হলুদ), ফলাফল ইতিবাচক হয়
কার্বন তারিখ হতে কোন কিছুর বয়স কত হতে হবে?
কার্বন-14 ডেটিং হল জৈবিক উৎপত্তির কিছু প্রত্নতাত্ত্বিক নিদর্শনের বয়স নির্ধারণ করার একটি উপায় যা প্রায় 50,000 বছর পুরনো। এটি হাড়, কাপড়, কাঠ এবং উদ্ভিদ তন্তুর মতো ডেটিং জিনিসগুলিতে ব্যবহৃত হয় যা তুলনামূলকভাবে সাম্প্রতিক অতীতে মানুষের কার্যকলাপ দ্বারা তৈরি হয়েছিল