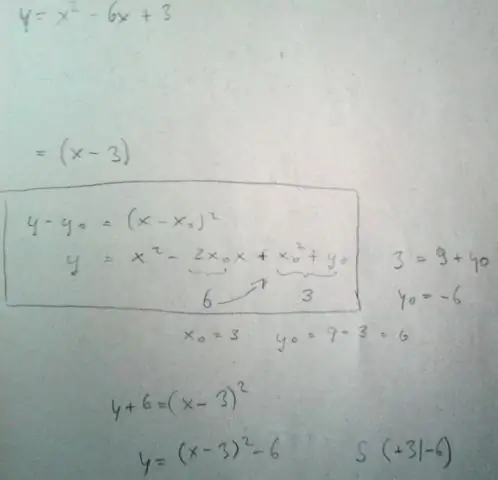
- লেখক Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:34.
- সর্বশেষ পরিবর্তিত 2025-06-01 05:03.
ক দ্বিঘাত ফাংশন একটি ফর্ম f(x) = ax2 + bx + c, যেখানে a, b, এবং c হল এমন সংখ্যা যার একটি শূন্যের সমান নয়। a এর গ্রাফ দ্বিঘাত ফাংশন একটি বক্ররেখাকে প্যারাবোলা বলা হয়। প্যারাবোলাগুলি ঊর্ধ্বমুখী বা নিম্নমুখী হতে পারে এবং "প্রস্থ" বা "খাড়া" পরিবর্তিত হতে পারে, তবে তাদের সকলের একই মৌলিক "U" আকৃতি রয়েছে।
এখানে, শীর্ষবিন্দু আকারে একটি কি?
y = a(x - h)2 + k, যেখানে (h, k) হল শীর্ষবিন্দু . তে "ক" শীর্ষবিন্দু ফর্ম একই "a" হিসাবে। y = কুঠার মধ্যে2 + bx + c (অর্থাৎ, উভয় a-এর মান ঠিক একই)। "a" এর চিহ্নটি আপনাকে বলে যে চতুর্ভুজটি খোলে নাকি নিচের দিকে খোলে।
আপনি কিভাবে একটি সমীকরণ নির্ধারণ করবেন একটি ফাংশন? এটা তুলনামূলকভাবে সহজ নির্ধারণ কিনা একটি সমীকরণ একটি ফাংশন y এর জন্য সমাধান করে। যখন আপনি একটি দেওয়া হয় সমীকরণ এবং x-এর জন্য একটি নির্দিষ্ট মান, সেই x-মানের জন্য শুধুমাত্র একটি সংশ্লিষ্ট y-মান থাকা উচিত। যেমন, y = x + 1 হল a ফাংশন কারণ y সবসময় x এর চেয়ে বড় হবে।
এইভাবে, আপনি কিভাবে একটি প্যারাবোলার জন্য একটি সমীকরণ লিখবেন?
জন্য প্যারাবোলাস যে পাশে খোলা, আদর্শ ফর্ম সমীকরণ হল (y - k)^2 = 4p(x - h)। আমাদের শীর্ষবিন্দু বা টিপ পরাবৃত্ত বিন্দু দ্বারা দেওয়া হয় (h, k)। জন্য প্যারাবোলাস যেটি উপরে এবং নীচে খোলে, ফোকাস পয়েন্টটি (h, k + p) দ্বারা দেওয়া হয়। জন্য প্যারাবোলাস যে পাশে খোলা, ফোকাস পয়েন্ট হল (h + p, k)।
দ্বিঘাত ফাংশনের আদর্শ রূপ কী?
ক দ্বিঘাত ফাংশন ইহা একটি ফাংশন ডিগ্রী দুই. a এর গ্রাফ দ্বিঘাত ফাংশন ইহা একটি পরাবৃত্ত . সাধারণ একটি দ্বিঘাত ফাংশনের ফর্ম f(x)=ax2+bx+c যেখানে a, b, এবং c বাস্তব সংখ্যা এবং a≠0। দ্য একটি দ্বিঘাত ফাংশনের আদর্শ রূপ হল f(x)=a(x−h)2+k।
প্রস্তাবিত:
নাল ফ্যাক্টর ল ব্যবহার করে আপনি কিভাবে একটি দ্বিঘাত সমীকরণ সমাধান করবেন?

এ থেকে আমরা অনুমান করতে পারি যে: যেকোনো দুটি সংখ্যার গুণফল যদি শূন্য হয়, তাহলে একটি বা উভয় সংখ্যাই শূন্য। অর্থাৎ, যদি ab = 0 হয়, তাহলে a = 0 বা b = 0 (যার মধ্যে a = b = 0 হওয়ার সম্ভাবনা রয়েছে)। একে বলা হয় নাল ফ্যাক্টর ল; এবং আমরা এটি প্রায়ই দ্বিঘাত সমীকরণ সমাধান করতে ব্যবহার করি
একটি দ্বিঘাত সমীকরণ উদাহরণ কি?

একটি দ্বিঘাত সমীকরণ হল দ্বিতীয় ডিগ্রির একটি সমীকরণ, যার অর্থ এটিতে অন্তত একটি পদ রয়েছে যা বর্গযুক্ত। স্ট্যান্ডার্ড ফর্ম হল ax² + bx + c = 0 সহ a, b, এবং c ধ্রুবক, বা সাংখ্যিক সহগ, এবং x একটি অজানা পরিবর্তনশীল। একটি পরম নিয়ম হল যে প্রথম ধ্রুবক 'a' শূন্য হতে পারে না
আপনি কিভাবে একটি দ্বিঘাত ফাংশনের প্রতীকী উপস্থাপনা খুঁজে পান?

দ্বিঘাত ফাংশনগুলিকে সমীকরণ দ্বারা প্রতীকীভাবে উপস্থাপন করা যেতে পারে, y(x) = ax2 + bx + c, যেখানে a, b, এবং c হল ধ্রুবক, এবং a ≠ 0. এই ফর্মটিকে স্ট্যান্ডার্ড ফর্ম হিসাবে উল্লেখ করা হয়
আপনি কিভাবে C++ এ একটি দ্বিঘাত সমীকরণ লিখবেন?
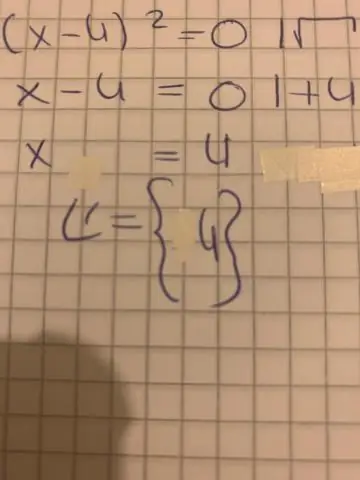
প্রোগ্রাম 2: একটি দ্বিঘাত সমীকরণে একটি b এবং c খুঁজুন #include #include int main(){float a,b,c; float d,root1,root2; printf('আক্স^2+bx+c বিন্যাসে দ্বিঘাত সমীকরণ লিখুন: '); scanf('%fx^2%fx%f',&a,&b,&c); d = b * b - 4 * a * c;
আপনি কিভাবে একটি দ্বিঘাত ফাংশনের সর্বোচ্চ মান খুঁজে পাবেন?

যদি আপনাকে সূত্র y = ax2 + bx + c দেওয়া হয়, তাহলে আপনি সূত্রটি max =c- (b2 / 4a) ব্যবহার করে সর্বোচ্চ মান খুঁজে পেতে পারেন। আপনার যদি y = a(x-h)2 + k সমীকরণ থাকে এবং থিয়েটারটি ঋণাত্মক হয়, তাহলে সর্বোচ্চ মান হল k
