সুচিপত্র:
ভিডিও: আপনি কিভাবে ডেরিভেটিভ মুখস্থ করবেন?
2024 লেখক: Miles Stephen | [email protected]. সর্বশেষ পরিবর্তিত: 2023-12-15 23:34
ভিডিও
এটি বিবেচনায় রেখে, আপনি কীভাবে ট্রিগ ফাংশনগুলি মুখস্থ করবেন?
ট্রিগ ফাংশনগুলির সংজ্ঞাগুলি কীভাবে মুখস্ত করবেন
- সোহ। সোহ - সাইন, কর্ণের বিপরীতে। sin(θ) = বিপরীত হাইপোটেনউজ।
- ক্যাহ. Cah – কোসাইন, কর্ণের উপর সংলগ্ন। cos(θ)=সংলগ্ন থাইপোটেনাস।
- তোয়া। Toa - স্পর্শক, সংলগ্ন উপর বিপরীত. tan(θ) = বিপরীত সংলগ্ন।
উপরের পাশাপাশি, ক্যালকুলাসের জন্য আমার কী মুখস্থ করতে হবে? ক্যালকুলাসের জন্য মুখস্থ করার জন্য দরকারী জিনিস
- পারস্পরিক পরিচয়।
- সংঘবদ্ধ পরিচয়।
- ভাগফলের পরিচয়।
- পিথাগোরিয়ান আইডেন্টিটিস।
- ডাবল অ্যাঙ্গেল আইডেন্টিটিস।
- বিজোড়-জোড় পরিচয়।
- সমষ্টি এবং পার্থক্য পরিচয়.
- হাফ অ্যাঙ্গেল আইডেন্টিটিস।
লোকেরা আরও জিজ্ঞাসা করে, আর্কসিনের ডেরিভেটিভ কী?
y = আর্কসিন (এক্স). sin(y) = sin( আর্কসিন (x)) = x। এর পরে, এই সূত্রের উভয় প্রান্তকে আলাদা করুন। আমরা বাম প্রান্তে চেইন নিয়ম প্রয়োগ করি, মনে রাখা যে অমৌলিক সাইন ফাংশনের কোসাইন ফাংশন এবং y হল x এর একটি পার্থক্যযোগ্য ফাংশন।
y = আর্কসিন (x) -1 x 1।
| d dx sin(y) | = | d dx x |
|---|---|---|
| cos(y) dy dx | = | 1 |
ক্যালকুলাসে চেইন নিয়ম কি?
দ্য চেইন নিয়ম বলে যে f(g(x)) এর ডেরিভেটিভ হল f'(g(x))⋅g'(x)। অন্য কথায়, এটি আমাদের *যৌগিক ফাংশন* পার্থক্য করতে সাহায্য করে। উদাহরণস্বরূপ, sin(x²) একটি যৌগিক ফাংশন কারণ এটি f(x)=sin(x) এবং g(x)=x² এর জন্য f(g(x)) হিসাবে তৈরি করা যেতে পারে।
প্রস্তাবিত:
আপনি কিভাবে একটি trig ফাংশন দ্বিতীয় ডেরিভেটিভ খুঁজে পাবেন?
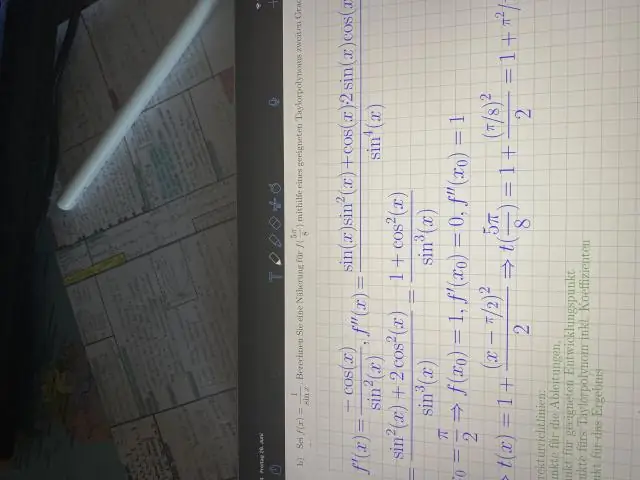
ভিডিও ঠিক তাই, 6টি ট্রিগ ফাংশনের ডেরিভেটিভ কি? ত্রিকোণমিতিক ফাংশনের ডেরিভেটিভস। মৌলিক ত্রিকোণমিতিক ফাংশন নিম্নলিখিত 6 ফাংশন অন্তর্ভুক্ত: sine ( পাপ x), কোসাইন ( কারণ x), স্পর্শক (tanx), cotangent (cotx), secant (secx) এবং cosecant (cscx)। এই সমস্ত ফাংশন তাদের ডোমেনে অবিচ্ছিন্ন এবং পার্থক্যযোগ্য। পরবর্তীকালে, প্রশ্ন হল, 1 এর ডেরিভেটিভ কি?
আপনি কিভাবে পর্যায় সারণী গান মুখস্থ করবেন?
ভিডিও সহজভাবে, আপনি কীভাবে পর্যায় সারণির প্রথম 20টি উপাদান মনে রাখতে পারেন? স্মৃতির যন্ত্র: হ্যাপি হেনরি আমাদের বন্ধু নেলি ন্যান্সি এমজিঅ্যালেনের কাছে বোরন কটেজের পাশে থাকেন। সিলি প্যাট্রিক কাছাকাছি থাকে। আর্থার কিস ক্যারি. এখানে তিনি বিছানার কাপড়ের নীচে শুয়ে আছেন, কিছুই নেই, নার্ভাস বোধ করছেন, দুষ্টু মার্গ্রেট সর্বদা দীর্ঘশ্বাস ফেলেন, "
আপনি কিভাবে সহজে মাইটোসিস মুখস্থ করবেন?
মাইটোসিসের পর্যায়: প্রোফেস, মেটাফেজ, অ্যানাফেজ, টেলোফেজ। সাইটোকাইনেসিস সাধারণত অ্যানাফেজ এবং/অথবা টেলোফেজের সাথে ওভারল্যাপ করে। আপনি বিখ্যাত স্মৃতিবিদ্যার সাথে পর্যায়গুলির ক্রম মনে রাখতে পারেন: [দয়া করে] MAT-তে প্রস্রাব করুন
আপনি কিভাবে মানচিত্র মুখস্থ করবেন?
পদ্ধতি 1 মহাদেশ অনুসারে মানচিত্র অধ্যয়ন করা। অভিভূত হওয়া থেকে বাঁচতে, অধ্যয়নের সময় একবারে শুধুমাত্র একটি বা দুটি মহাদেশে ফোকাস করুন। আপনার চিহ্নিত করতে সমস্যা হয় এমন দেশগুলিকে অগ্রাধিকার দিন। নিজেকে বর্ণানুক্রমিকভাবে কুইজ করুন। বর্তমান ইভেন্টে টাই। Loci পদ্ধতি ব্যবহার করুন. একটি স্মৃতির যন্ত্র তৈরি করুন
আপনি কিভাবে মাইটোসিস মুখস্থ করবেন?
মাইটোসিসের পর্যায়: প্রোফেস, মেটাফেজ, অ্যানাফেজ, টেলোফেজ। সাইটোকাইনেসিস সাধারণত অ্যানাফেজ এবং/অথবা টেলোফেজের সাথে ওভারল্যাপ করে। আপনি বিখ্যাত স্মৃতিবিদ্যার সাথে পর্যায়গুলির ক্রম মনে রাখতে পারেন: [দয়া করে] MAT-তে প্রস্রাব করুন