
- লেখক Miles Stephen [email protected].
- Public 2023-12-15 23:34.
- সর্বশেষ পরিবর্তিত 2025-01-22 16:56.
একটি যুক্তিসঙ্গত ” সংখ্যা দুটি পূর্ণসংখ্যার মধ্যে অনুপাত। জন্য উদাহরণ , নিম্নলিখিত হয় মূলদ সংখ্যা , এবং তাদের কোনোটিই পূর্ণসংখ্যা নয়: 1 / 2. 2 / 3।
এছাড়াও প্রশ্ন হল, পূর্ণ সংখ্যা নয় এমন মূলদ সংখ্যা কী?
সব ঋণাত্মক পূর্ণসংখ্যা হয় মূলদ সংখ্যা কিন্তু তারা হয় পূর্ণ সংখ্যা নয় . যেমন-3 হল a মূলদ সংখ্যা (-3/1 হিসাবে প্রকাশ করা যেতে পারে), কিন্তু এটি একটি পূর্ণ সংখ্যা না . ভগ্নাংশ যেমন 1/2, -3/4, 22/7 ইত্যাদি।
দ্বিতীয়ত, ঋণাত্মক 3 কি একটি মূলদ সংখ্যা? - 3 নেতিবাচক তাই এটি প্রাকৃতিক বা সম্পূর্ণ নয় সংখ্যা . মূলদ সংখ্যা হয় সংখ্যা যেটিকে দুটি পূর্ণসংখ্যার ভগ্নাংশ বা অনুপাত হিসাবে প্রকাশ করা যেতে পারে। মূলদ সংখ্যা Q দ্বারা চিহ্নিত করা হয়। যেহেতু - 3 − হিসাবে লেখা যেতে পারে 3 1, এটা যুক্তি হতে পারে যে − 3 এছাড়াও একটি বাস্তব সংখ্যা.
দ্বিতীয়ত, একটি মূলদ সংখ্যা কী যা একটি পূর্ণ সংখ্যা?
প্রতি সম্পূর্ণ নম্বর ইহা একটি মূলদ সংখ্যা : উদাহরণস্বরূপ, 3=31। সুতরাং এটাই যুক্তিসঙ্গত . প্রতি সম্পূর্ণ নম্বর n কে পূর্ণসংখ্যার ভগ্নাংশ হিসাবে লেখা যেতে পারে: n=n1। আমাদের এইভাবে লিখতে হবে না; আমাদের শুধু জানতে হবে যে প্রতিটি প্রকাশ করা সম্ভব সম্পূর্ণ নম্বর পূর্ণসংখ্যার ভগ্নাংশ হিসাবে, এবং তাই এটি যুক্তিসঙ্গত.
একটি মূলদ সংখ্যা কি একটি পূর্ণ সংখ্যা হতে পারে কিন্তু একটি পূর্ণসংখ্যা নয়?
এর সেট পুরো সংখা = {0, 1, 2, 3, 4, …} পুরো সংখা ঠিক আছে পূর্ণসংখ্যা যেগুলো অ-নেতিবাচক। সেট স্বরলিপি ব্যবহার করে, আমরা করতে পারা যে সেট বলতে পূর্ণসংখ্যা যখন এর সেট পুরো সংখা মূলত হয় তাই প্রশ্নে ফিরে আসা; না , এখানে কোনো মূলদ সংখ্যা নেই যা একটি পূর্ণসংখ্যা নয় কিন্তু ইহা একটি সম্পূর্ণ নম্বর.
প্রস্তাবিত:
উদাহরণসহ প্রাকৃতিক সংখ্যা ও পূর্ণ সংখ্যা কী?
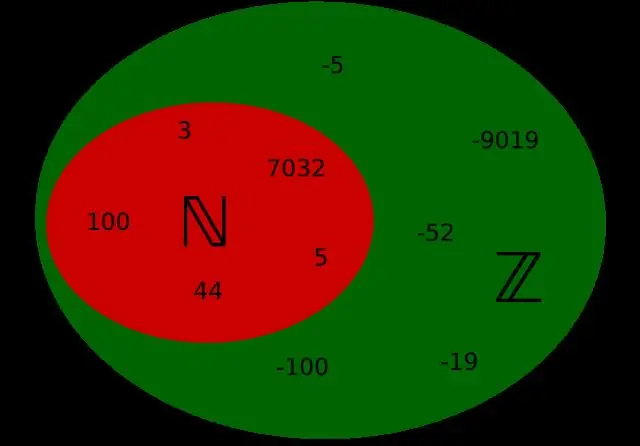
প্রাকৃতিক সংখ্যা হল সমস্ত সংখ্যা 1, 2, 3, 4… এগুলি হল সংখ্যাগুলি যা আপনি সাধারণত গণনা করেন এবং সেগুলি অনন্ত পর্যন্ত চলতে থাকবে। পূর্ণ সংখ্যা হল 0 সহ সমস্ত প্রাকৃতিক সংখ্যা যেমন 0, 1, 2, 3, 4… পূর্ণসংখ্যা সমস্ত পূর্ণ সংখ্যা এবং তাদের ঋণাত্মক প্রতিরূপ যেমন
কোন ধরনের সংখ্যা মিলে সংখ্যার সেটকে প্রকৃত সংখ্যা বলা হয়?

বাস্তব সংখ্যা সেট (ধনাত্মক পূর্ণসংখ্যা) বা পূর্ণ সংখ্যা {0, 1, 2, 3,} (অ ঋণাত্মক পূর্ণসংখ্যা)। গণিতবিদরা উভয় ক্ষেত্রেই 'প্রাকৃতিক' শব্দটি ব্যবহার করেন
প্রাকৃতিক সংখ্যা পূর্ণ সংখ্যা পূর্ণসংখ্যা এবং মূলদ সংখ্যা কি?

প্রকৃত সংখ্যাগুলি প্রধানত মূলদ এবং অমূলদ সংখ্যায় শ্রেণীবদ্ধ করা হয়। মূলদ সংখ্যা সব পূর্ণসংখ্যা এবং ভগ্নাংশ অন্তর্ভুক্ত. সমস্ত ঋণাত্মক পূর্ণসংখ্যা এবং পূর্ণ সংখ্যা পূর্ণসংখ্যার সেট তৈরি করে। পূর্ণ সংখ্যা সমস্ত প্রাকৃতিক সংখ্যা এবং শূন্য নিয়ে গঠিত
প্রাকৃতিক সংখ্যা এবং পূর্ণ সংখ্যার মধ্যে কোন সংখ্যাটি সাধারণ নয়?

শূন্যের কোনো ইতিবাচক বা ঋণাত্মক মান নেই। যাইহোক, শূন্য একটি পূর্ণ সংখ্যা হিসাবে বিবেচিত হয়, যার ফলে এটি একটি পূর্ণসংখ্যা হয়, তবে অগত্যা একটি স্বাভাবিক সংখ্যা নয়
প্রতিটি প্রাকৃতিক সংখ্যা কি একটি পূর্ণ সংখ্যা?

হ্যাঁ এটা সত্য. কারণ প্রাকৃতিক সংখ্যা 1 থেকে শুরু হয় এবং অসীমে শেষ হয় যেখানে পূর্ণ সংখ্যা 0 থেকে শুরু হয় এবং অসীমে শেষ হয়। 0 হল একমাত্র সংখ্যা যা সম্পূর্ণ সংখ্যা কিন্তু স্বাভাবিক সংখ্যায় নয়। তাই প্রতিটি স্বাভাবিক সংখ্যাই একটি পূর্ণ সংখ্যা
