
- লেখক Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:34.
- সর্বশেষ পরিবর্তিত 2025-01-22 16:56.
উদাহরণ 1 নীচের সিরিজটি অভিসারী কিনা তা নির্ধারণ করুন বা divergent . এই ফাংশনটি স্পষ্টভাবে ধনাত্মক এবং যদি আমরা x xকে বড় করে হর করি ইচ্ছাশক্তি বড় হও তাই ফাংশনও কমে যাচ্ছে। দ্য অবিচ্ছেদ্য হয় divergent এবং সিরিজটিও তাই divergent দ্বারা ইন্টিগ্রেল টেস্ট.
এর পাশে, e x কনভারজেন্ট নাকি ডাইভারজেন্ট?
1/( প্রাক্তন ) বড় বা সমান 1/( প্রাক্তন +1) (শূন্য এবং অসীমের মধ্যে) অনুপযুক্ত অবিচ্ছেদ্য ∫∞01( প্রাক্তন )d এক্স হয় অভিসারী এবং এটি 1 তবে, অনুপযুক্ত অবিচ্ছেদ্য ∫∞01( প্রাক্তন +1) ঘ এক্স হয় divergent.
কেউ জিজ্ঞাসা করতে পারে, উদাহরণ সহ অনুচিত অবিচ্ছেদ্য কি? একটি অনুপযুক্ত অবিচ্ছেদ্য একটি নির্দিষ্ট অবিচ্ছেদ্য যেটির হয় বা উভয় সীমা অসীম বা একটি ইন্টিগ্র্যান্ড যা ইন্টিগ্রেশনের পরিসরে এক বা একাধিক পয়েন্টে অসীমের কাছে যায়। অনুপযুক্ত ইন্টিগ্রেল একটি সাধারণ Riemann ব্যবহার করে গণনা করা যাবে না অবিচ্ছেদ্য . জন্য উদাহরণ , দ্য অবিচ্ছেদ্য.
দ্বিতীয়ত, ক্যালকুলাসে কনভারজেন্স এবং ডাইভারজেন্স কী?
সিরিজ কনভারজেন্স এবং ডাইভারজেন্স - সংজ্ঞা A সিরিজ Σa একটি যোগফল S-তে রূপান্তরিত হয় যদি এবং শুধুমাত্র যদি আংশিক যোগফলের ক্রম S-তে রূপান্তরিত হয়। অর্থাৎ, নিম্নলিখিত সীমাটি বিদ্যমান থাকলে একটি সিরিজ একত্রিত হয়: অন্যথায়, যদি s-এর সীমাk (k → ∞ হিসাবে) অসীম হয় বা অস্তিত্বে ব্যর্থ হয়, তারপর সিরিজটি ভিন্ন হয়ে যায়।
1 ইনফিনিটির মান কত?
মূলত, 1 খুব বড় সংখ্যা দিয়ে ভাগ করলে শূন্যের খুব কাছাকাছি চলে যায়, তাই… 1 দ্বারা বিভক্ত অনন্ত , যদি আপনি আসলে পৌঁছাতে পারেন অনন্ত , 0 এর সমান।
প্রস্তাবিত:
জলের অণুগুলির মধ্যে হাইড্রোজেন বন্ধন কীভাবে বাষ্পীভবনের আগে প্রচুর পরিমাণে শক্তি শোষণ করার জলের ক্ষমতা ব্যাখ্যা করতে সহায়তা করতে পারে?
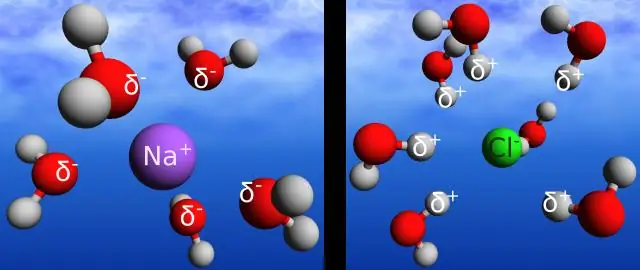
পানিতে থাকা হাইড্রোজেন বন্ধন এটিকে অন্যান্য অনেক পদার্থের তুলনায় তাপ শক্তিকে আরও ধীরে ধীরে শোষণ করতে এবং ছেড়ে দিতে দেয়। তাপমাত্রা হল অণুর গতির (গতিশক্তি) পরিমাপ। গতি বাড়ার সাথে সাথে শক্তি বেশি হয় এবং এইভাবে তাপমাত্রাও বেশি হয়
রাসায়নিক বিক্রিয়া ঘটেছে কিনা তা নির্ধারণ করতে আপনি পাঁচ ধরনের প্রমাণ কী ব্যবহার করতে পারেন?

রাসায়নিক পরিবর্তনের কিছু লক্ষণ হল রঙের পরিবর্তন এবং বুদবুদের গঠন। রাসায়নিক পরিবর্তনের পাঁচটি শর্ত: রঙ পরিবর্তন, একটি বর্ষণ গঠন, একটি গ্যাস গঠন, গন্ধ পরিবর্তন, তাপমাত্রা পরিবর্তন
জ্যামিতিক বৈশিষ্ট্য প্রমাণ করার জন্য কোন প্রমাণ একটি স্থানাঙ্ক সমতলে পরিসংখ্যান ব্যবহার করে?

একটি প্রমাণ যা জ্যামিতিক বৈশিষ্ট্য প্রমাণ করার জন্য একটি স্থানাঙ্ক সমতলে পরিসংখ্যান ব্যবহার করে তাকে ত্রিকোণমিতিক হিসাবে উল্লেখ করা হয়
কিভাবে সমন্বয় সমতল আপনাকে সংশ্লিষ্ট পক্ষগুলি সমতুল্য নির্ধারণ করতে সাহায্য করতে পারে?

একটি স্থানাঙ্ক সমতলে দুটি ত্রিভুজ দেওয়া হলে, আপনি তাদের বাহুর দৈর্ঘ্য খুঁজে বের করতে দূরত্ব সূত্র ব্যবহার করে তারা সঙ্গতিপূর্ণ কিনা তা পরীক্ষা করতে পারেন। যদি তিন জোড়া বাহু সর্বসম হয়, তবে ত্রিভুজগুলি উপরের উপপাদ্য দ্বারা সর্বসম হয়
স্ট্রিক পরীক্ষা কিভাবে খনিজ সনাক্ত করতে সহায়ক হতে পারে?

'স্ট্রিক টেস্ট' হল একটি পদ্ধতি যা গুঁড়ো আকারে খনিজটির রঙ নির্ধারণ করতে ব্যবহৃত হয়। স্ট্রিক পরীক্ষাটি 'স্ট্রিক প্লেট' নামে পরিচিত আনগ্লাজড চীনামাটির একটি টুকরো জুড়ে খনিজটির একটি নমুনা স্ক্র্যাপ করে করা হয়। এটি প্লেটের পৃষ্ঠে অল্প পরিমাণে গুঁড়ো খনিজ তৈরি করতে পারে
