ভিডিও: আপনি কিভাবে হার্ডি ওয়েইনবার্গ সমস্যা সমাধান করবেন?
2024 লেখক: Miles Stephen | [email protected]. সর্বশেষ পরিবর্তিত: 2023-12-15 23:34
ভিডিও
এর পাশে, হার্ডি ওয়েইনবার্গে আপনি কীভাবে পি এবং কিউ খুঁজে পাবেন?
থেকে পি = 1 - q এবং q জানা যায়, এটা সম্ভব গণনা পি যেমন. জানা p এবং q , এই মানগুলি প্লাগ করা একটি সহজ ব্যাপার হার্ডি - ওয়েইনবার্গ সমীকরণ (p² + 2pq + q² = 1)। এটি তখন জনসংখ্যার মধ্যে নির্বাচিত বৈশিষ্ট্যের জন্য তিনটি জিনোটাইপের পূর্বাভাসিত ফ্রিকোয়েন্সি সরবরাহ করে।
দ্বিতীয়ত, হার্ডি ওয়েইনবার্গ কেন গুরুত্বপূর্ণ? গুরুত্ব : দ্য হার্ডি - ওয়েইনবার্গ মডেলটি আমাদেরকে সময়ের সাথে সাথে একটি জনসংখ্যার প্রকৃত জেনেটিক কাঠামোর সাথে তুলনা করতে সক্ষম করে যেটি আমরা আশা করব যদি জনসংখ্যা ছিল হার্ডি - ওয়েইনবার্গ ভারসাম্য (অর্থাৎ, বিকশিত নয়)। প্রশ্নঃ আমরা কিভাবে ব্যবহার করি হার্ডি - ওয়েইনবার্গ জিনোটাইপ এবং অ্যালিল ফ্রিকোয়েন্সি ভবিষ্যদ্বাণী করার মডেল?
এছাড়াও জানুন, আপনি কীভাবে হার্ডি ওয়েইনবার্গ সমীকরণটি ব্যবহার করবেন?
দ্য হার্ডি - ওয়েইনবার্গ সমীকরণ . জেনেটিক ভারসাম্যের জনসংখ্যার জন্য: p + q = 1.0 (উভয় অ্যালিলের ফ্রিকোয়েন্সির যোগফল 100%।)
কেন হার্ডি ওয়েইনবার্গ দরকারী?
অবিশ্বাস্যভাবে হয় দরকারী কারণ এটি গাণিতিকভাবে একটি জনসংখ্যার জেনেটিক পণ্যকে বর্ণনা করে যেখানে সমস্ত ব্যক্তির বেঁচে থাকার এবং বেঁচে থাকা সন্তান উৎপাদনের সমান সম্ভাবনা রয়েছে। বিশেষত, এটি জিনোটাইপ ফ্রিকোয়েন্সিগুলি গণনা করে যা একটি জনসংখ্যার মধ্যে পরিলক্ষিত হবে যা বিকশিত হচ্ছে না।
প্রস্তাবিত:
আপনি কিভাবে একটি অনুপাত সমস্যা সমাধান করবেন?
প্রথমে অনুপাত লিখুন, অনুপস্থিত পদের জন্য দাঁড়ানোর জন্য একটি চিঠি ব্যবহার করে। আমরা 20 বার x, এবং 50 গুণ 30 গুণ করে ক্রস পণ্যগুলি খুঁজে পাই। তারপর x বের করতে ভাগ করি। এই ধাপটি ঘনিষ্ঠভাবে অধ্যয়ন করুন, কারণ এটি এমন একটি কৌশল যা আমরা প্রায়শই বীজগণিতে ব্যবহার করব
আপনি কিভাবে পদার্থবিদ্যার গতি সংক্রান্ত সমস্যা সমাধান করবেন?
1-মাত্রিক সমস্যা সমাধানের ধাপগুলি সমস্যাটি আপনাকে যে পরিমাণ দেয় তা লিখুন (প্রাথমিক এবং চূড়ান্ত অবস্থান, প্রাথমিক এবং চূড়ান্ত বেগ, ত্বরণ, সময়, ইত্যাদি) আপনি কোন পরিমাণ খুঁজে বের করার চেষ্টা করছেন তা লিখুন। এই পরিমাণগুলিকে সম্পর্কিত করার জন্য গতিশীল সমীকরণ (বা কখনও কখনও দুটি সমীকরণ) খুঁজুন। বীজগণিত সমাধান করুন
আপনি কিভাবে একটি ঢাল সমস্যা সমাধান করবেন?
ঢাল চিহ্নিত করুন, মি. এটি ঢাল সূত্র ব্যবহার করে লাইনের দুটি পরিচিত বিন্দুর মধ্যে ঢাল গণনা করে করা যেতে পারে। y-ইন্টারসেপ্ট খুঁজুন। এটি ঢাল-ইন্টারসেপ্ট সূত্রে লাইনে একটি বিন্দু (x, y) এর ঢাল এবং স্থানাঙ্ক প্রতিস্থাপন করে এবং তারপর b এর সমাধান করে করা যেতে পারে
আপনি কিভাবে সীমিত প্রতিক্রিয়াশীল ভর ভর সমস্যা সমাধান করবেন?
প্রতিটি বিক্রিয়াক যে পরিমাণ পণ্য উৎপাদন করবে তা গণনা ও তুলনা করে সীমিত বিকারকটি খুঁজুন। রাসায়নিক বিক্রিয়ার জন্য রাসায়নিক সমীকরণ ভারসাম্য। প্রদত্ত তথ্যকে মোলে রূপান্তর করুন। উত্পাদিত পণ্যের ভর খুঁজে পেতে প্রতিটি পৃথক বিক্রিয়াকের জন্য স্টোইচিওমেট্রি ব্যবহার করুন
আপনি কিভাবে একটি সিরিজ সার্কিট সমস্যা সমাধান করবেন?
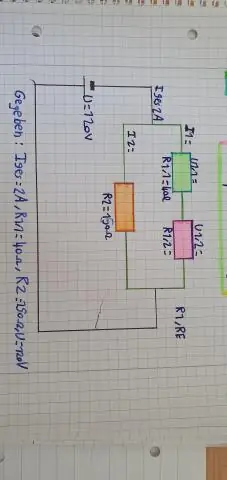
ভিডিও শুধু তাই, একটি সিরিজ সার্কিট উদাহরণ কি? একটি উদাহরণ এর a সিরিজ বর্তনী ক্রিসমাস লাইট একটি স্ট্রিং. যদি কোন একটি বাল্ব অনুপস্থিত হয় বা পুড়ে যায়, কোন কারেন্ট প্রবাহিত হবে না এবং কোন আলো জ্বলবে না। সমান্তরাল সার্কিট এগুলি ছোট রক্তনালীগুলির মতো যা একটি ধমনী থেকে প্রবাহিত হয় এবং তারপরে হৃৎপিণ্ডে রক্ত ফেরত দেওয়ার জন্য একটি শিরার সাথে সংযুক্ত হয়। একটি সিরিজ সার্কিট দেখতে কেমন?